机器视觉与图像处理___2025-04-06
绪论
机器视觉 与 计算机视觉
- 机器视觉: 机器视觉系统中一定包含硬件, 需要 图像处理模块
- 计算机视觉: 不一定包含硬件, 偏算法
模式识别
模式识别研究各类模式的分类
图像模式的分类是机器视觉的一个重要问题
模式识别中的许多方法可以用于机器视觉中
图像处理
图像处理: 输入图像到另一种图像的转换
和机器视觉的最大区别:
- 机器视觉: 机器是图像的解释者
- 图像处理: 人是最终的解释者
图像
分类
| 分类依据 | 分类1 | 分类2 |
|---|---|---|
| 存在形式 | 物理图像: 物质或能量的实际分布 | 抽象图像: “数学图像 |
| 色彩特性 | 彩色图像: 图像每个点有多种局部特征 | 灰阶图像: 每个像素点只有一个亮度值 |
| 光谱特性 | 可见光图像 红外线图像 | 雷达图像 声纳图像 |
| 时间特性 | 动态图像: 随时间变化的图像 | 静止图像: 不随时间变化的图像 |
图像的表达式
通用表达式:
$$ I = f(x, y, z, \lambda, t) $$
简化式: $$ I = f(x, y) $$
- 其中:
- $x, y, z$: 空间坐标
- $\lambda$: 波长
- $t$: 时间
数字图像
- 物体图像的数字化表示
- 时间与空间的非连续函数(信号)
- 便于计算机处理
- 离散单元: 像素的集合
数字图像处理
- 精度高
- 处理内容丰富
- 复杂非线性处理, 处理灵活
- 再现性好
缺点: 速度有限, 实时性差
图像的基本运算
数字化(采样和量化)
经典均匀采样:
$$ f_d(x,y) = \begin{cases}
f_c(x,y) & \text{if } x=i\Delta x, y=j\Delta y \
0 & \text{else}
\end{cases} $$
- 其中:
- $x = i\Delta x, y = j\Delta y$
量化: $$ \text{if } f_i \leq f < f_{i+1} \ \text{then } g = g_i $$
坐标运算
-
平移变换
$$ x’ = x + T_x \ y’ = y + T_y \ \begin{bmatrix} x’ & y’ & 1 \end{bmatrix} = \begin{bmatrix} x & y & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \ 0 & 1 & 0 \ T_x & T_y & 1 \end{bmatrix} $$ -
比例变换 $$ x’ = S_x x \ y’ = S_y y \ \begin{bmatrix} x’ & y’ & 1 \end{bmatrix} = \begin{bmatrix} x & y & 1 \end{bmatrix} \begin{bmatrix} S_x & 0 & 0 \ 0 & S_y & 0 \ 0 & 0 & 1 \end{bmatrix} $$
-
旋转变换 $$ x’ = x \cos \theta - y \sin \theta \ y’ = x \sin \theta + y \cos \theta \ \begin{bmatrix} x’ & y’ & 1 \end{bmatrix} = \begin{bmatrix} x & y & 1 \end{bmatrix} \begin{bmatrix} \cos \theta & \sin \theta & 0 \ -\sin \theta & \cos \theta & 0 \ 0 & 0 & 1 \end{bmatrix} $$
-
对称变换
- 关于x轴对称 $$ \begin{bmatrix} 1 & 0 & 0 \ 0 & -1 & 0 \ 0 & 0 & 1 \end{bmatrix} $$
- 关于y轴对称 $$ \begin{bmatrix} -1 & 0 & 0 \ 0 & 1 & 0 \ 0 & 0 & 1 \end{bmatrix} $$
- 关于原点对称 $$ \begin{bmatrix} -1 & 0 & 0 \ 0 & -1 & 0 \ 0 & 0 & 1 \end{bmatrix} $$
- 关于y=x对称 $$ \begin{bmatrix} 0 & 1 & 0 \ 1 & 0 & 0 \ 0 & 0 & 1 \end{bmatrix} $$
- 关于y=-x对称 $$ \begin{bmatrix} 0 & -1 & 0 \ -1 & 0 & 0 \ 0 & 0 & 1 \end{bmatrix} $$
-
错切变换 $$ x’ = x + b y \ y’ = c x + y \ \begin{bmatrix} x’ & y’ & 1 \end{bmatrix} = \begin{bmatrix} x & y & 1 \end{bmatrix} \begin{bmatrix} 1 & b & 0 \ c & 1 & 0 \ 0 & 0 & 1 \end{bmatrix} $$
沿着x轴错切, $b = 0$, 图像横过来歪斜 沿着y轴错切, $c = 0$, 图像竖过来歪斜
算数运算
多图像平均, 二次曝光…
消除背景
逻辑运算
与 或 补(非) 异或
图像点运算
灰度变换
灰度变换函数: 一种映射关系记为"T算子” $$ g(x,y) = T[f(x,y)] $$
典型灰度变换函数
三个典型的灰度变换函数:
 a. 图像求反: 黑白翻转, 即黑白底片和照片的关系
a. 图像求反: 黑白翻转, 即黑白底片和照片的关系
b. 增强对比度: 增加相邻部分之间的灰度差别
c. 动态范围压缩: 牺牲动态范围从而在特定设备上呈现
直方图
对图像各灰度值的统计特性, 统计出现次数
除以图像的面积即可得到 图像的概率密度函数PDF
特点:
- 灰度分布规律的反映
- 与视觉感受有一致性
- 图像的直方图唯一, 直方图对应图像不唯一
- 反映整体, 不反映细节
反映总体的特性:
- 明暗程度
- 细节清晰程度
- 动态范围大小
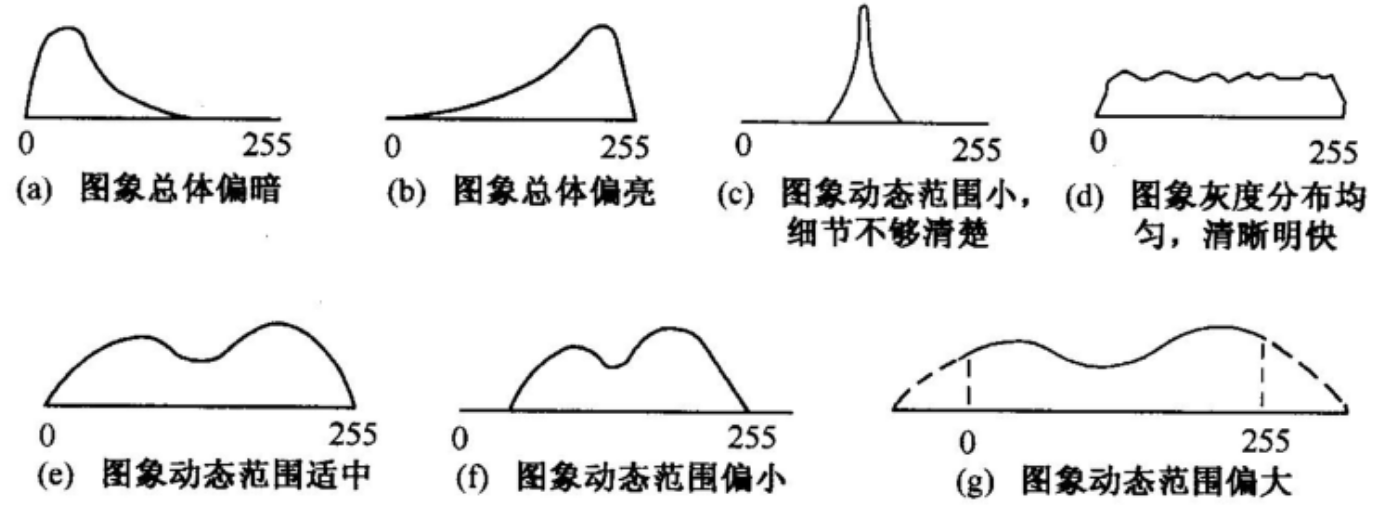
直方图变换: $ s = T(r) $
需满足:
- 单调性: 在 $ 0 \leq r \leq 1 $ 内, $ T(r) $ 严格单调递增
- 对于 $ 0 \leq r \leq 1 $, $ T(r) $ 的值域为 $ 0 \leq T(r) \leq 1 $
直方图均衡
直方图均衡化: 将原图像的直方图变换成均匀分布的直方图
变量定义:
- $ p_r(r) $: 原图像的灰度概率密度函数
- $ p_s(s) $: 均衡化后的灰度概率密度函数
- $ s $: $r$ 的累积概率密度函数
变换函数为: $ s = T(r) = \int_0^r p_r(w) dw $
直方图均衡化表格方法见书 P44
直方图匹配/规定
指对图像变换, 直至其直方图形状与规定的直方图相匹配
具体步骤
- $r$ 映射为 $s$: $s = T(r) = \int_0^r p(w) dw$
- $z$ 映射为 $v$: $v = G(z) = \int_0^z q(w) dw$
- 根据 $v=G(z), z=G^{-1}(v)$
由于 $v$ $s$ 分布相同, 逐一取 $v = s$
求出 $z$ 的反函数 $z = G^{-1}(v)$
PPT P77 的表格方法很详细
直方图对比
判定图像的内容的相似度
比较方法一般有:
- 卡方
- 相关性
- 交叉熵
- 巴氏距离
直方图投影
获取ROI, 并实现 标注/识别/测量
反向投影定义: 用输入图像的像素对应直方图一个bin上的像素值
案例:
-
灰度图像: $$ Image = \begin{bmatrix} 0 & 1 & 2 & 3 \ 4 & 5 & 6 & 7 \ 8 & 9 & 10 & 11 \ 8 & 9 & 14 & 15 \end{bmatrix} $$
-
bin指定区间为[0, 3), [4, 7), [8, 11), [12, 16) -
直方图: $$ Histogram = \begin{bmatrix} 4 & 4 & 6 & 2 \end{bmatrix} $$
-
反向投影: $$ BackProjection = \begin{bmatrix} 4 & 4 & 4 & 4 \ 4 & 4 & 4 & 4 \ 6 & 6 & 6 & 6 \ 6 & 6 & 2 & 2 \end{bmatrix} $$
图像滤波
图像处理范畴, 将图片视为2D信号, 用信号处理的方法进行处理
像素间的概念
- 邻域: 一个像素
p的临近的像素集合- 4-邻域: 上下左右(
r像素) - 8-邻域: 上下左右 + 对角线(
s像素)
- 4-邻域: 上下左右(
- 邻接: 两个像素邻接就看是否接触
- 连接: 邻接的同时, 灰度值满足相似准则(一般是灰度值相同, 或是都在一个灰度集合
V中)- 4-连接: 2个像素
p & r在V中, 且r在$N_4(p)$中 - 8-连接: 2个像素
p & r在V中, 且r在$N_8(p)$中
邻接是连接的必要非充分条件
- 4-连接: 2个像素
- 连通: 连通区域是所有彼此连通的像素的一条通路
- 4-通路, 8-通路: 定义同上
对于一个图像中的两个子集
S & T, 如果S的一个或多个像素与T的一个或多个像素连通, 则称S与T连通(邻接/连接)
像素距离的度量
- 欧式距离: $D_E(p,q) = \sqrt{(x_p - x_q)^2 + (y_p - y_q)^2}$
- 城市街区距离: $D_4(p,q) = |x_p - x_q| + |y_p - y_q|$
- 棋盘距离: $D_8(p,q) = \max(|x_p - x_q|, |y_p - y_q|)$
一个函数f(x)的范数($m$表示指标):
$$ ||f||m = \left[ \int{-\infty}^{\infty} |f(x)|^m dx \right]^{\frac{1}{m}} $$
模板运算
- 模板卷积
用一个模板(卷积核)在图像上滑动, 将模板中心与图像中的每个像素重合, 然后进行乘积运算, 结果相加后输出 - 模板排序
将模板框选的像素值取出并排序, 然后根据排序结果选择一个序号, 输出该序号对应的像素值
3x3空域滤波模板一般表述形式:
$$ R = w_1z_1 + w_2z_2 + … + w_9z_9 = \sum_{i=1}^{9} w_iz_i $$
- 边界处处理
边界处处理方式:- 忽略
- 取4-邻接的值
- 周期循环
- 外插
- 模板分类
- 平滑模板
- 锐化模板
- 线性模板
- 非线性模板
线性平滑滤波
- 领域平均: $g(x,y) = \frac{1}{M} \sum_{(n,m) \in s} f(n,m)$
- 加权平均: $g(x,y) = \sum_{i=-m}^{m} \sum_{j=-n}^{n} w(i,j)f(x+i,y+j)$
- 高斯平滑: 计算量极大, 要将
2-D的卷积核转换为1-D的卷积核
非线性平滑滤波
利用统计特性去除噪声点
- 中值滤波:
$Y_i = \text{median}(X_{i-k}, X_{i-(k-1)}, …, X_{i+k})$
窗口长度 $n = 2k+1$
注意:
- 中值滤波对孤立噪声有良好的滤除作用
- 有尖顶几何特征的, 一般采用十字形窗口, 大小不超过最小有效物体
- 有较多[点/线/尖顶]的, 不宜采用中值滤波
-
最大最小滤波 中值可被视为是50%的序统计滤波器
最大滤波是 100% 的序统计滤波器, 保留亮点, 消除暗淡的噪声
最小滤波是 0% 的序统计滤波器, 保留暗点, 消除明亮的噪声 -
最频值滤波 最频值滤波取窗口内像素值出现次数最多的值
其特点是可以锐化目标边缘, 且对脉冲噪声有良好的滤除作用中值总比均值更接近最频值
空域平滑滤波总结:
- 低通滤波器
- 要求行列数为奇数
- 去噪能力与模板大小有关
- 具有平滑效果
锐化滤波
目的是加强 目标边界 和 图像细节
-
一阶微分算子 / 梯度算子 $$ \nabla f = \begin{bmatrix} \frac{\partial f}{\partial x} \ \ \frac{\partial f}{\partial y} \end{bmatrix} = \begin{bmatrix} G_x \ G_y \end{bmatrix} $$
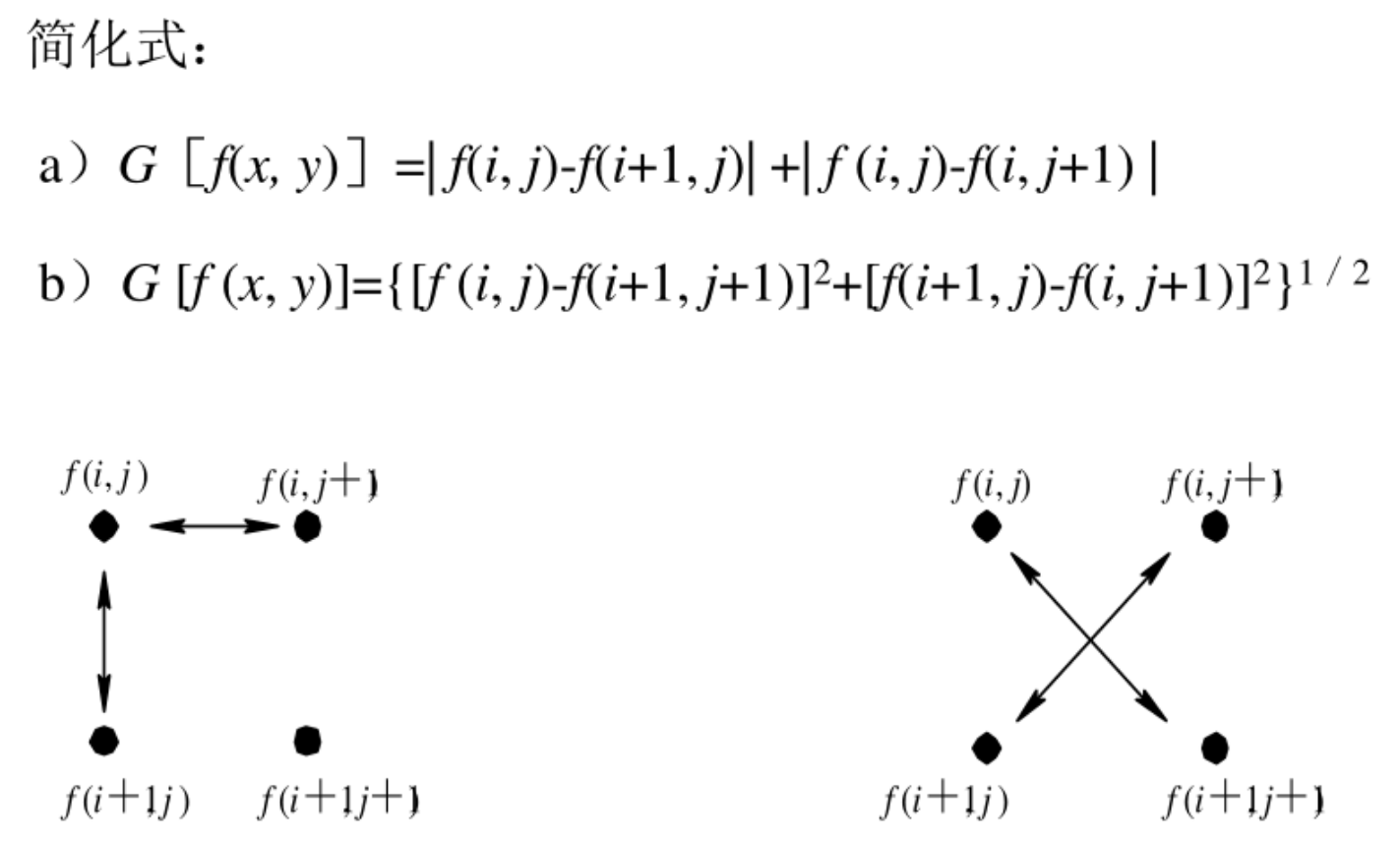
模板:
- Robert: $$ \begin{bmatrix} 1 & 0 \ 0 & -1 \end{bmatrix} $$
- Prewitt: $$ \begin{bmatrix} 1 & 0 & -1 \ 1 & 0 & -1 \ 1 & 0 & -1 \end{bmatrix} $$
- Sobel: $$ \begin{bmatrix} 1 & 0 & -1 \ 2 & 0 & -2 \ 1 & 0 & -1 \end{bmatrix} $$
-
二阶微分算子 / 拉普拉斯算子 $$ \nabla^2 f = \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2} $$
典型的Laplacian模板: $$ \begin{bmatrix} 0 & 1 & 0 \ 1 & -4 & 1 \ 0 & 1 & 0 \end{bmatrix} \quad \begin{bmatrix} 1 & 1 & 1 \ 1 & -8 & 1 \ 1 & 1 & 1 \end{bmatrix} \quad \begin{bmatrix} 1 & -2 & 1 \ -2 & 4 & -2 \ 1 & -2 & 1 \end{bmatrix} $$
锐化滤波总结:
- 锐化滤波器是高通滤波器, 可去模糊, 增强边缘和细节
- 使用微分运算实现高频增强
- 一阶 阶跃边缘 检测能力强
- 二阶 细线增强 和 去聚焦模糊 效果好
- 空域高通对噪声放大严重
非线性锐化滤波
- 非线性锐化滤波器
- 非线性锐化滤波器是高通滤波器
- 使用非线性运算实现高频增强
频域图像增强
离散傅里叶变换
- 1-D DFT $$ F(u) = \sum_{x=0}^{N-1} f(x) e^{-j\frac{2\pi}{N}ux} $$
- 1-D IDFT $$ f(x) = \frac{1}{N} \sum_{u=0}^{N-1} F(u) e^{j\frac{2\pi}{N}ux} $$
- 2-D DFT $$ F(u,v) = \frac{1}{N} \sum_{x=0}^{N-1} \sum_{y=0}^{N-1} f(x,y) e^{-j\frac{2\pi}{N}(ux + vy)} $$
- 2-D IDFT $$ f(x,y) = \frac{1}{N} \sum_{u=0}^{N-1} \sum_{v=0}^{N-1} F(u,v) e^{j\frac{2\pi}{N}(ux + vy)} $$
性质
-
可分离性
按 行和列 可以实现 两次 1-D DFT 计算 2-D DFT $$ F(u,v) = F_x\left{F_y\left[f(x,y)\right]\right} \ = F_y\left{F_x\left[f(x,y)\right]\right} $$ -
平移性
傅里叶变换对平移不敏感(幅值不变) $$ f(x,y) \rightarrow f(x-a,y-y_0) \ \rightarrow F(u,v) \rightarrow F(u,v)e^{-j\frac{2\pi}{N}(ux_0 + vy_0)} $$ -
旋转不变性
傅里叶变换对旋转不敏感 $$ f(r, \theta + \theta_0) \leftrightarrow F(w, \phi + \theta_0) $$ -
剪切性
$$ f(x+by, y) \leftrightarrow F(u, v-bu) \ f(x, y+dx) \leftrightarrow F(u-dv, v) $$ -
共轭对称性
傅里叶变换是共轭对称的 $$ \begin{cases} x = r\cos\theta \ y = r\sin\theta \end{cases} \quad \begin{cases} u = w\cos\phi \ v = w\sin\phi \end{cases} \ f(r, \theta + \theta_0) \leftrightarrow F(w, \phi + \theta_0) $$ -
周期性
傅里叶变换是周期函数(图像本身也可以被看作周期函数) $$ F(u+aN,v+bN) = F(u,v) \ f(x+aN,y+bN) = f(x,y) $$ -
共轭对称性 傅里叶变换是共轭对称的 $$ f^(x,y) \leftrightarrow F^(-u,-v) $$
-
线性 $$ F{af(x,y) + bg(x,y)} = aF{f(x,y)} + bF{g(x,y)} $$
-
比例变换性 $$ af(x,y) \leftrightarrow aF(u,v) \ f(ax,by) \leftrightarrow \frac{1}{|ab|}F\left(\frac{u}{a},\frac{v}{b}\right) $$
-
均值性 $$ \frac{1}{N^2} \sum_{x=0}^{N-1} \sum_{y=0}^{N-1} f(x,y) = \bar{f}(x,y) = F(0,0) $$
-
卷积定理
$F$ 的大小是 $A \times B$, $G$ 的大小是 $C \times D$
两者卷积结果大小定为 $M \times N$
满足 $M \geq A + C - 1, N \geq B + D - 1$
先要对$F$和$G$进行0填充, 均扩充为$M \times N$
则卷积结果为: $$ f(x,y) * g(x,y) = \frac{1}{MN} \sum_{m=0}^{M-1} \sum_{n=0}^{N-1} F(m,n)G(x-m,y-n) \ \leftrightarrow F(u,v) \cdot G(u,v) $$ -
相关 $$ f(x,y) \circ g(x,y) = \sum_{m=0}^{M-1} \sum_{n=0}^{N-1} f(m,n)g(x+m,y+n) \ \leftrightarrow F(u,v) \cdot G^*(u,v) $$
频域滤波流程
- 输入图像中心移位变换: $$ f(x,y) \rightarrow f(x,y)\cdot(-1)^{x+y} $$
- 计算1的DFT: $$ f(x,y)\cdot(-1)^{x+y} \rightarrow F(u,v) $$
- 设计滤波器与DFT的乘积: $$ F(u,v) \cdot H(u,v) $$
- 计算IDFT后保留实部
- 再进行中心移位变换(乘系数), 得到滤波增强后的$g(x,y)$
空域和频域滤波之间的联系:
- 二维卷积定理
- 傅里叶变换对:
$$ f(x,y) * h(x,y) \leftrightarrow F(u,v) \cdot H(u,v) \ f(x,y) \cdot h(x,y) \leftrightarrow F(u,v) * H(u,v) $$
频域高低通滤波器
-
低通滤波器: $$ ILPF: H(u,v) = \begin{cases} 1, & \text{if } D(u,v) \leq D_0 \ 0, & \text{if } D(u,v) > D_0 \end{cases} $$ 低通的脉冲响应会造成 振铃现象:
- $D_0$ 越小, 同心环越少而宽, 模糊加重
- 图像的能量绝大部分集中于低频, 高频能量相对较少, 滤除高频成分会造成图像模糊
-
巴特沃斯低通滤波器: $$ BLPF: H(u,v) = \frac{1}{1 + \left[{D(u,v)}/{D_0}\right]^{2n}} $$
- 阶数$n$ 越大, 越接近理想低通滤波器, 振铃现象越明显
- 阶数$n$ 取1, 无振铃现象
-
指数(高斯)滤波器: $$ ELPF: H(u,v) = e^{-\left[{D(u,v)}/{D_0}\right]^n} $$
- 高斯低通滤波器没有振铃现象
- 高斯低通滤波器是 巴特沃斯低通滤波器的近似
- 下降的更快, 导致更多高频信息损失, 导致细节丢失, 画面更模糊
- 尾部较长, 对噪声的衰减能力大于巴特沃斯, 但因此平滑效果不如巴特沃斯
-
高通滤波器: 以上三种低通滤波器, 取反即可, 或将$D_0$和$D(u,v)$互换
-
高频提升: $f_{hp}(x,y) = Af(x,y) - f_{lp}(x,y)$
-
高频加强: $H’(u,v) = H(u,v) + c, c \in (0,1)$
频域选择性滤波
带阻滤波器: $$ IBSF: H(u,v) = \begin{cases} 0, & \text{if } | D(u,v) - D_0| \leq W/2 \ 1, & \text{else} \end{cases} $$ $$ BBSF: H(u,v) = \frac{1}{1 + \left[\frac{DW}{D^2-D_0^2}\right]^{2n}} $$ $$ GBSF: H(u,v) = 1- e^{-\left[\frac{D^2 - D_0^2}{DW}\right]^n} $$
可用于去除正弦噪声污染
同态滤波
同态滤波是将图像分解为 入射照度 和 反射分量 的乘积
入射照度$i(x,y)$: 由光源决定 (单位 $lx$ 勒克斯)
反射分量$r(x,y)$: 由物体表面特性决定, $ r(x,y) \in (0,1) $
先对图像进行对数变换, 然后进行频域滤波, 最后再进行指数变换 $$ \ln f(x,y) = \ln[i(x,y)r(x,y)] = \ln[i(x,y)] + \ln[r(x,y)] \ H(u,v)F(u,v) = H(u,v)I(u,v) + H(u,v)R(u,v) \ g(x,y) = exp|h_i(x,y)| \cdot exp|h_r(x,y)| \ $$
$H(u,v)$ 即同态滤波函数:
- 照度分量 变化较缓慢, 对应低频部分
- 反射分量 在材质的交界处剧变, 对应高频部分
同态滤波可同时实现: 亮度范围压缩, 对比度增强
图像恢复
图像恢复的定义
图像退化 即图像的质量降低, 不同退化类型的图像恢复方法不同:
| 退化类型 | 恢复方法 |
|---|---|
| 模糊 | 滤波 |
| 失真 | 校正 |
| 投影 | 重建 |
复原 vs 增强 都可以改善图像质量
改善方法:
- 图像增强: 突出感兴趣的特征
- 图像复原: 恢复图像的原始特征, 以保真为前提 评价标准:
- 图像增强: 视觉效果, 提高可理解性
- 图像复原: 提高视感质量
图像退化数学模型
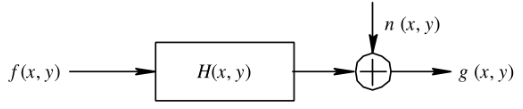
通用的图像退化模型:
$$ g(x,y) = H\left[f(x,y)\right] + n(x,y) $$
退化系统若满足以下4个性质, 恢复会相对容易:
- 线性: $H\left[k_1f_1(x,y) + k_2f_2(x,y)\right] = k_1H\left[f_1(x,y)\right] + k_2H\left[f_2(x,y)\right]$
- 相加性: $H\left[f_1(x,y) + f_2(x,y)\right] = H\left[f_1(x,y)\right] + H\left[f_2(x,y)\right]$
- 一致性: $H\left[kf(x,y)\right] = kH\left[f(x,y)\right]$
- 位置(空间)不变性: $H\left[f(x-a,y-b)\right] = g(x-a, y-b)$
若线性退化系统满足后三个性质, 则称为线性空间不变系统, 有: $$ g(x,y) = f(x,y) * h(x,y) + n(x,y) \ G(u,v) = F(u,v)H(u,v) + N(u,v) $$
常见的噪声&概率密度函数(PDF):
| 噪声类型 | 说明 | |
|---|---|---|
| 高斯(正态)噪声 | $p(z) = \frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(z-\mu)^2}{2\sigma^2}}$ | 最理想的临界模型 |
| 瑞利噪声 | $p(z) = \begin{cases} \frac{2}{b}(z-a)e^{-{(z-a)^2}/{b}}, & z \geq a \ 0, & \text{else} \end{cases}$ | 近似有偏斜的直方图 |
| 伽玛&指数分布 | $p(z) = \begin{cases} \frac{a^bz^{b-1}}{(b-1)!} e^{-az}, & z \geq 0 \ 0, & \text{else} \end{cases}$ | $ \mu = b/a; \ \sigma^2 = b / a^2; \ a,b > 0; b \in Z \ \text{对于指数, 取} b = 1$ |
| 均匀密度分布 | $p(z) = \begin{cases} \frac{1}{b-a}, & a \leq z \leq b \ 0, & \text{else} \end{cases}$ | $ \mu = (a+b)/2; \ \sigma^2 = (b-a)^2/12$ |
| 脉冲(椒盐)噪声 | $p(z) = \begin{cases} P_a, & z = a \ P_b, & z = b \ 0, & \text{else} \end{cases}$ | $P_a + P_b = 1$ |
| 周期噪声 |
滤波器自学part
考题: 既要去除噪声, 又要保持足够多的边缘信息
可以采用双边滤波器. 双边滤波器是一种非线性的图像滤波方式,它能够在平滑图像的同时保留边缘信息。双边滤波器使用二维高斯函数生成距离模板,并使用一维高斯函数生成值域模板。这种滤波器同时结合了图像的空间邻近度和像素值相似度,以达到保边去噪的目的。
也可以采用自适应中值滤波器, 当标准中值滤波器输出为最值时, 扩大尺寸并重复判断. 当输出不为最值时, 判断当前像素是否为脉冲, 若是脉冲, 输出中值, 否则直接输出当前值, 从而保持边缘. 采用自适应中值滤波器可以滤除脉冲噪声, 平滑非脉冲噪声的同时, 减少对目标边界造成的失真
非约束复原
图像退化模型: $ n = g - Hf $
由于对$n$没有先验知识, 目标化为寻找$\hat{f}$使得$H\hat{f}$在均方误差意义下接近$g$, 即
$$|n|^2 = |g - H\hat{f}|^2 \
= (g-H\hat{f})^T(g-H\hat{f}) $$
因此, 恢复问题的求解就化为 对 $\hat{f}$ 求满足下式的最小值
$$ L(\hat{f}) = |g - H\hat{f}|^2 $$
求微分并令其为0, 可得 无约束恢复公式:
$$ \hat{f} = (H^TH)^{-1}H^Tg = H^{-1}g$$
逆滤波
逆滤波是一种简单直接的 无约束图像恢复方法
不考虑噪声, 可近似认为: $ F(u,v) = \frac{G(u,v)}{H(u,v)} $
考虑噪声后的逆滤波形式为:
$$ G(u,v) = F(u,v)H(u,v) + N(u,v) \
F(u,v) = \frac{G(u,v)}{H(u,v)} + \frac{N(u,v)}{H(u,v)} $$
$H(u,v)$ 随着原点距离的增加而迅速减小, 但噪声变化缓慢
这会导致噪声项变得很大
因此一般恢复只能在与原点较近, 接近频域中心的范围进行
病态特性:
- $H(u,v)$ 出现零点会导致不稳定解
- 零点出现将会放大噪声项
对策:
- 有约束图像复原
- 限制在频谱坐标离远点不太远的有限区域内
为了改进, 引入 恢复转移函数 $M(u,v)$

$$ M(u,v) = \begin{cases} k, & \text{if } H(u,v) \leq d \ \frac{1}{H(u,v)}, & \text{else} \end{cases} \ M(u,v) = \begin{cases} 1, & \text{if } u^2+v^2 > w_0^2 \ \frac{1}{H(u,v)}, & \text{else} \end{cases} $$
前者的$k$和$d$均小于1, $d$较小为佳
后者的$w_0$目的是去除零点, 缺点是振铃效应明显
所谓的约束是指: 是否考虑图像的物理约束
例如空域平滑, 灰度值为正
最小二乘类有约束复原
最小二乘类约束复原公式: 寻找最优估计 $\hat{f}$, 使得$J(\hat{f})$最小
$$J(\hat{f}) = ||Q\hat{f}||^2 + \alpha(||g-h\hat{f}||^2-||n||^2)$$
从而得到 有约束恢复公式
$$ \hat{f} = (h^Th + \gamma Q^TQ)^{-1}h^Tg $$
其中, $\gamma = 1/\alpha$
维纳滤波器
维纳滤波器是一种最小均方误差滤波器, 目标是使得复原后的图像$\hat{f}(x,y)$与原始图像均方误差最小, 即:
$$ E\left{\left[\hat{f}(x,y) - f(x,y)\right]^2\right} = min $$
图像的功率谱随着频率的升高而下降
噪声往往具有平坦的功率谱
因此, 可以认为:
- 功率谱的低频部分以图像信号为主
- 功率谱的高频部分以噪声为主
$$\hat{F}(u,v) = \left[\frac{H^*(u,v)}{|H(u,v)|^2 +\gamma \frac{S_n(u,v)}{S_f(u,v)}}\right]G(u,v)$$
其中:
- $S_f(u,v)$: 信号的相关矩阵元素的傅里叶变换
- $S_n(u,v)$: 噪声的相关矩阵元素的傅里叶变换
分析:
- 当$\gamma = 1$时, 为经典维纳滤波器, 否则称为 参变维纳滤波器
- 无噪声
- $S_n(u,v) = 0$, 则$\hat{F}(u,v) = H^*(u,v)/|H(u,v)|^2 = 1/H(u,v)$
- 称为理想反向滤波器
- 由于噪声的统计性质未知, 可以近似为:
$$ \hat{F}(u,v) = \frac{H^*(u,v)}{|H(u,v)|^2 + K}G(u,v) $$
其中$K$表示噪声对信号的频谱密度之比(即信噪比)
平滑约束最小二乘复原
拉普拉斯算子$\Delta^2$可以突出边缘, 并恢复图像的平滑性
在离散的情况下, 可以用差分运算实现, 记拉普拉斯算子扩展到图像尺寸的函数对应的2-D傅里叶变换为P(u,v)
从而, 可以得到:
$$ \hat{F}(u,v) = \frac{1}{N^2} \frac{H^*(u,v)}{|H(u,v)|^2 + \gamma |P(u,v)|^2}G(u,v) \quad u,v=0,1,…,N-1$$
该滤波器也称 最小平方滤波器
相较于维纳滤波器, 该滤波器除均值和方差的估计之外, 无需其他统计参数的知识
图像校正和修补
几何失真
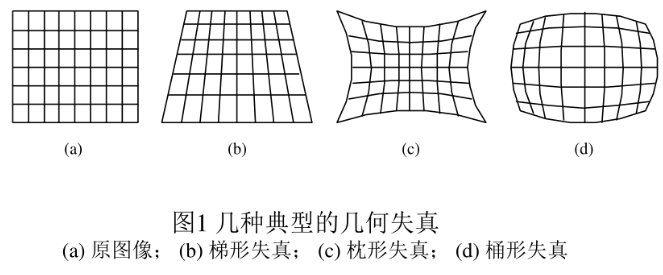
校正步骤:
- 空间变换: 对像素重新排列以恢复空间关系
- 灰度插值: 变换后的像素赋予灰度值以恢复灰度值
空间变换模型
- 刚性变换: 仅改变图像的位置和角度, 维持原始形状 $$ \begin{bmatrix} x_2 \ y_2 \end{bmatrix} = \begin{bmatrix} \cos\theta \plusmn \sin\theta \ \sin\theta \plusmn \cos\theta \end{bmatrix} \begin{bmatrix} x_1 \ y_1 \end{bmatrix} + \begin{bmatrix} t_x \ t_y \end{bmatrix} $$
- 仿射变换: 在刚性的基础上, 增加了尺度变换和剪切操作, 可以被视为是 平移/缩放/旋转/剪切 变换的综合
$$ \begin{bmatrix} x_2 \ y_2 \end{bmatrix} = \begin{bmatrix} a_{11} & a_{12} \ a_{21} & a_{22} \end{bmatrix} \begin{bmatrix} x_1 \ y_1 \end{bmatrix} + \begin{bmatrix} a_{13} \ a_{23} \end{bmatrix} $$ - 投影变换: 三维图像投影到二维平面 $$ \begin{bmatrix} x_2 \ y_2 \ 1 \end{bmatrix} = \begin{bmatrix} a_{11} & a_{12} & a_{13} \ a_{21} & a_{22} & a_{23} \end{bmatrix} \begin{bmatrix} x_1 \ y_1 \ 1 \end{bmatrix} +\begin{bmatrix} x_1 \ y_1 \end{bmatrix} $$
- 非刚性/弹性变换: 直线在变换后可能变成一条曲线, 通过函数来实现
几何畸变
记基准图像的坐标系统为$(x,y)$, 畸变图像的坐标系统为$(x’,y’)$. 则其关系可用解析式表示: $$x’ = h_1(x,y) \ y’ = h_2(x,y)$$
通常采用多项式表示: $$x’ = \sum_{i=0}^{N-1} \sum_{j=0}^{M-1} a_{ij}x^iy^j \ y’ = \sum_{i=0}^{N-1} \sum_{j=0}^{M-1} b_{ij}x^iy^j$$
常用线性畸变近似较小的几何畸变(即三角形线性法) $$x’ = a_0 + a_1x + a_2y \ y’ = b_0 + b_1x + b_2y$$
可以用二次型来更精确地近似 $$x’ = a_0 + a_1x + a_2y + a_3x^2 + a_4xy + a_5y^2 \ y’ = b_0 + b_1x + b_2y + b_3x^2 + b_4xy + b_5y^2$$
对于四边形的几何失真, 常用 双线性等式: $$x’ = k_1x + k_2y + k_3xy + k_4\ y’ = k_5x + k_6y + k_7xy + k_8$$
该等式用于描述畸变过程, 左侧为畸变图像坐标, 右侧为基准图像坐标
- 三角形线性法
取出基准图的三个点与畸变图的三个点一一对应, 联立方程组即可解出6个系数 - 同理, 采用二次型, 则需要解出
12个系数
灰度差值
- 线性插值: 使用连接两个已知量的直线, 来估计已知量之间的未知量的值
- 最近邻差值: 取离目标点最近的已知点的值作为目标点的值
- 双线性插值: 先在x方向上进行线性插值, 然后在y方向上进行线性插值
- 三次线性插值: 使用三次函数(16个系数)
图像重建
投射断层成像
原理: 从发射源射出的光线经过物体后, 形成图像 $$I = I_0exp\left(-\int_0^L k(s)ds\right)$$ 其中,
- $I_0$为射线源的强度
- $k(s)$为物体s沿着射线方向的衰减系数
- $L$为物体的厚度(辐射的射线)
- $I$为穿过的光线的强度
其余成像方式不作考点
投影重建
假定有个点源, 其距离原点距离为$r$, 投影的中心距离为$s$, 存在 $s=r\sin\theta$, 那么有基本模型:
$$ p(s,\theta) = \int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty} f(x,y) \delta( x\cos\theta + y\sin\theta - s)dxdy $$
上式可等价表示为:
$$ g(s,\theta) = \int_{(s,\theta)} f(x,y) dt \
= \int_{-\infty}^{+\infty} f(s\cos\theta - t\sin\theta, s\sin\theta + t\cos\theta) dt $$
其中, $t(s)=\sqrt{1-s^2} \quad |s|\leq1$, 表示投影方向
两个式子是从不同的角度出发, 但本质上是一样的
上式作为平面积分来看待, 下式作为线积分来看待
推理过程借助坐标变换实现: $$ \begin{bmatrix} s \ t \end{bmatrix} = \begin{bmatrix} \cos\theta & \sin\theta \ -\sin\theta & \cos\theta \end{bmatrix} \begin{bmatrix} x \ y \end{bmatrix} $$
反投影
得到投影数据后, 直接将一个坐标对应的x和y方向的投影数据相加, 最后归一化得到估计数据
对于3x3的图像, 9个未知数对应6个投影数据, 本就是无法准确得出原结果的, 因此必然存在误差, 并非逆运算
光晕效果 的产生是因为 相当于采用了低通滤波器, 这导致了高频信息的丢失, 边界模糊
Randon拉东变换
线积分: $R_f(p,\theta) = \int_{-\infty}^{+\infty} f(x,y) dl$
直线$l$的方程: $p = x\cos\theta + y\sin\theta$
上式可等价表示为:
可以视为对二维图像在射线方向上的线积分
中心层定理
对$f(x,y)$直接2-DFT中取出的一个切面 与 $f(x,y)$先进行Randon变换后的1-DFT, 结果一致
据此, 重建思路: 各个面上的投影1-DFT结果叠加, 之后做2-IDFT, 即可得到重建图像
$$P(w,\theta) = $$
针对光晕, 提出两种方案
- 逆投影滤波 对傅里叶"图像", 乘以系数$\sqrt{w_x^2 + w_y^2}$, 使得高频部分的影响减小
该系数也称斜坡滤波器
- 滤波逆投影重建 FBP(重点) 先对投影数据$p(s,\theta)$的1-DFT$P(w,\theta)$乘以$|w|$, 然后再进行2-IDFT, 使得高频部分的影响减小
顺序互换可以有很多的方法, 但本质就是
- 滤波
- 投影和反投影
- 做傅里叶变换
逆投影滤波重建
- 由投影数据 $p(s,\theta)$ 做逆投影得到二维傅里叶图像
- 对二维傅里叶图像, 乘以斜坡滤波器 $\sqrt{w_x^2 + w_y^2}$
- 对乘积做2-IDFT, 得到重建图像
卷积逆投影重建
- 得到投影数据 $p(s, \theta)$ 后, 以
s为变量, 做1-D FT得到 $P(w, \theta)$ - 乘以 斜坡滤波器 $|w| = \sqrt{u^2+v^2}$, 得到 $Q(w, \theta)$
- 求 $Q(w, \theta)$ 的
1-D IFT, 得到 $q(s, \theta)$ - 由 $q(s, \theta)$ 做逆投影, 得到重建图像
考试复习
书上原题很多, 以书为主 恢复和重建 证明题 中心 拉东必要
第一章
简答
第二章
加减乘除, 灰度变换(计算题), 直方图均衡 有 局限性 => 规定化
第三章
模板运算(必考)
第四章
2-D DFT
图像恢复
恢复和增强的联系
退化的模型和逆滤波的对应
病态性 => 维纳滤波 和 巴特沃斯
推导不要求
校正和修复
为了实现, 要做哪些核心步骤
每个步骤的目的和效果
自学part
投影重建
各种投影重建的联系, 8-12作业? 要求理论推导
扇束和代数是不要求的
视觉系统
8分
基本组件, 应用场景的特点
联系方式
13818921596 changqing@ecust.edu.cn